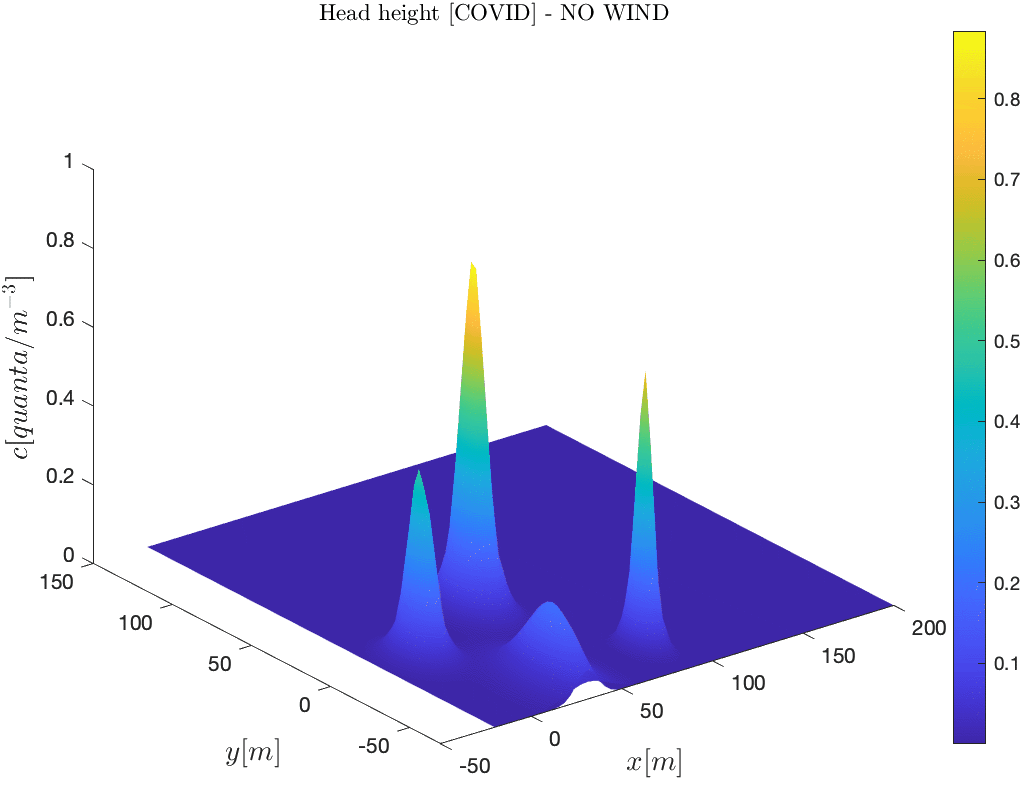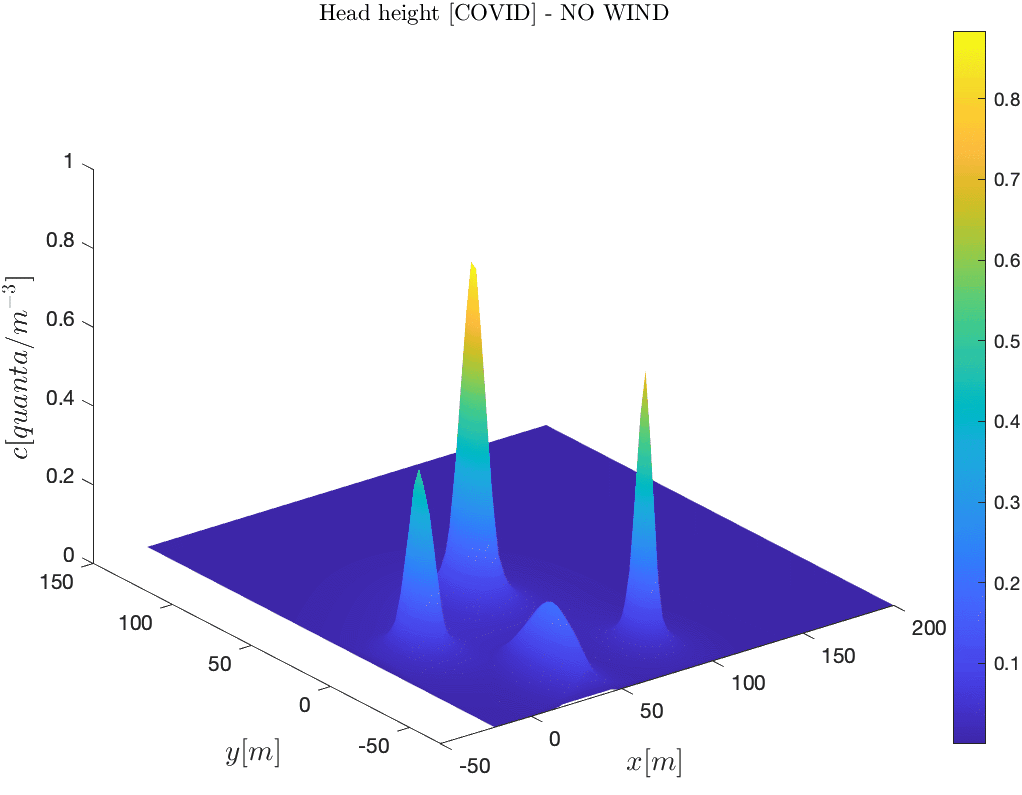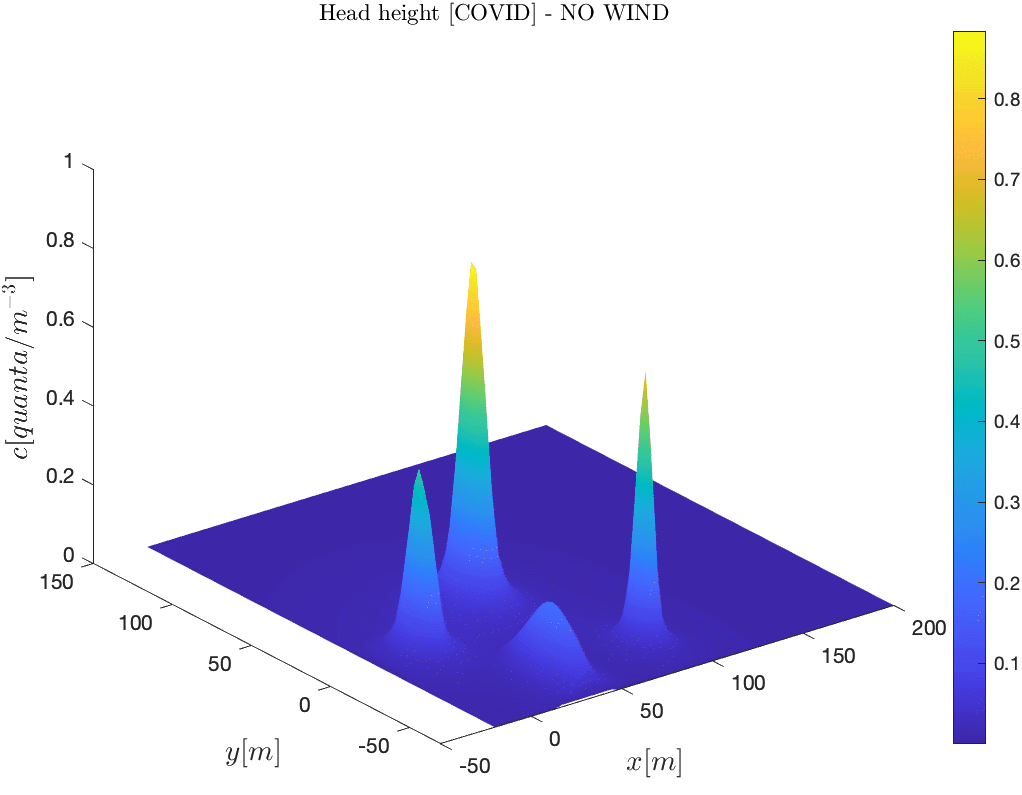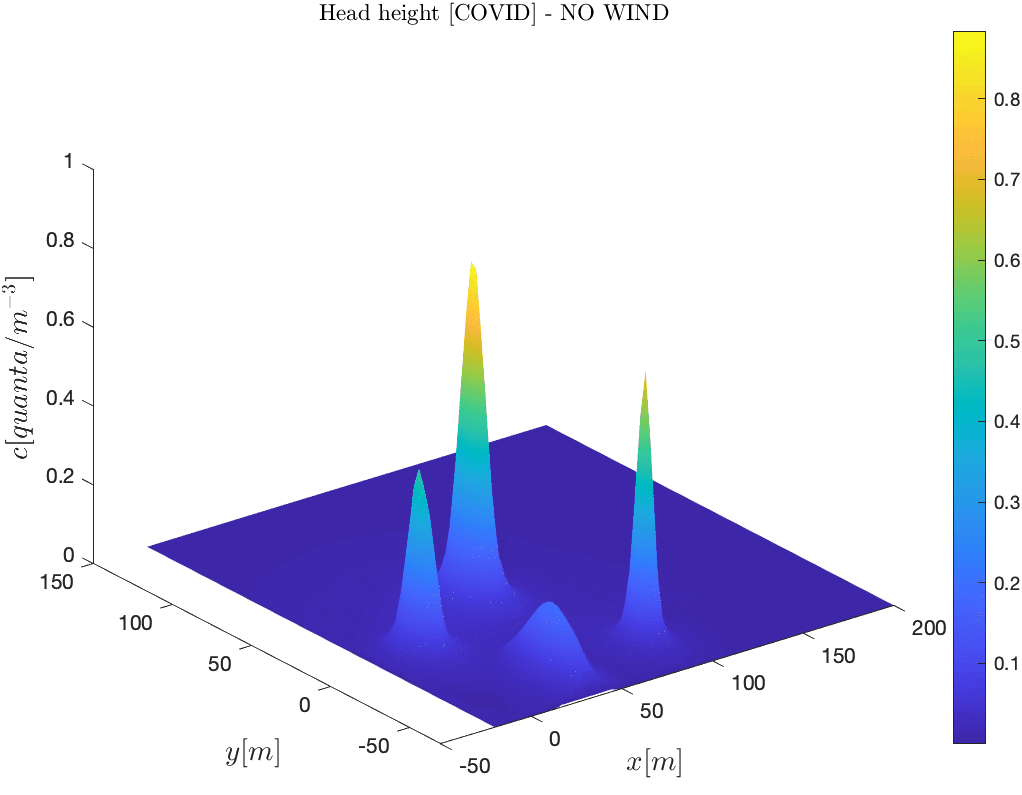
In the following simulation, 5 infected concert-goers are considered as distinct sources fixed in space. Using the analytical solution for advection-diffusion of a Gaussian plume, and at increasing times, two scenarios are considered: NO WIND and WIND. The standard advection-diffusion-reaction model deals with the time evolution of the virus in air. The mathematical equations describing this evolution are partial differential equations derived from mass balances. The overall change in concentration is described by the 2-D advection-diffusion equation:

\[ \frac{\partial}{\partial t} \left\langle\bar{C}(x,y,t) \right\rangle+\frac{\partial}{\partial x} \left(u(x,y)\left\langle\bar{C}(x,y,t) \right\rangle\right) + \frac{\partial}{\partial y}\left(v(x,y)\left\langle\bar{C}(x,y,t) \right\rangle \right) = \frac{\partial}{\partial x} \left(D_x \frac{\partial}{\partial x}\left\langle\bar{C}(x,y,t) \right\rangle\right) + \frac{\partial}{\partial y} \left(D_y \frac{\partial}{\partial y}\left\langle\bar{C}(x,y,t) \right\rangle\right) \]
\[x, y \in \mathbb{R} , t\geq0\]

The solution for the continuous release of COVID in two dimensions is given by: \[ C(x,y,t)= \frac{\dot{M}}{2\,\sqrt{{\pi}^2\,\sigma^2_x\,\sigma^2_y}}{e}^{-\frac{{\left(X-U_x\,t\right)}^2}{2\,\sigma^2_x}-\frac{{\left(Y-U_y\,t\right)}^2}{2\,\sigma^2_y}} \]